Giới thiệu
Loạt bài "Máy học phổ thông"
Loạt bài Máy học phổ thông nhằm vào một mục tiêu đơn giản là diễn giải một số kỹ thuật máy học với kiến thức toán phổ thông mà học sinh phổ thông trung học (cấp 3, khoảng lớp 11, 12) có thể hiểu, và áp dụng ngay lập tức. Dĩ nhiên, vì đây là trang mạng của nhóm Python cho người Việt nên ngôn ngữ lập trình được chọn để thể hiện các kỹ thuật trong loạt bài này sẽ là ngôn ngữ Python.
Máy học
Máy học (machine learning) là một nhánh khoa học máy tính tận dụng các kỹ thuật tính toán để tạo cho máy tính khả năng "học" từ dữ liệu, mà không cần phải được lập trình rõ ràng. Một số ví dụ ứng dụng máy học bao gồm việc phỏng đoán giá nhà dựa trên diện tích đất, tự động phân loại hoa từ kích thước cánh, hoặc tự tìm đường nhanh nhất để thoát khỏi mê cung.
Máy học thường được chia làm ba nhóm chính:
- Có giám sát (supervised)
- Các kỹ thuật trong nhóm này tận dụng sự hiện diện của kết quả gốc để điều chỉnh việc học của máy tính. Ví dụ như giá nhà đã bán gần đây có thể giúp cho việc dự đoán giá già sẽ bán được trong tương lai.
- Không giám sát (unsupervised)
- Các kỹ thuật trong nhóm này không sử dụng kết quả gốc nhưng vẫn có thể phân loại dữ liệu đầu vào thành nhiều nhóm riêng biệt. Ví dụ như các loại hoa có thể được phân loại theo kích thước cánh hoa to hay nhỏ, dài hay ngắn một cách tự động mà không cần bất kỳ chỉ dẫn cụ thể nào.
- Củng cố (reinforcement)
- Sự phối hợp giữa học có giám sát, và học không giám sát tạo ra các kỹ thuật học củng cố trong đó kết quả gốc chỉ được sử dụng sau khi một loạt các lựa chọn đã xảy ra. Ví dụ trong khi tìm đường thoát khỏi mê cung, chỉ sau khi tìm được đường đến cửa ra thì ta mới biết con đường đã đi là con đường tốt.
Hồi quy tuyến tính
Một trong các kỹ thuật phổ dụng nhất trong máy học là kỹ thuật phân tích hồi quy tuyến tính (linear regression). Tên gọi này có hai phần quan trọng:
- Hồi quy (regression)
- Phân tích hồi quy cho phép ta tìm ra quan hệ giữa các biến độc lập (giả sử là \(x_1, x_2, \dots, x_n\)) và biến phụ thuộc (giả sử là \(y\)). Bình thường chúng ta sẽ có sẵn mối quan hệ \(y = f(x_1, x_2, \dots, x_n)\) để từ đó xác định giá trị của biến phụ thuộc theo biến độc lập. Mục tiêu của phân tích hồi quy là tìm mối quan hệ từ các giá trị của biến độc lập và biến phụ thuộc.
- Tuyến tính (linear)
- Trong hồi quy tuyến tính, mối quan hệ giữa các biến độc lập và biến phụ thuộc được giả định là một mối quan hệ tuyến tính. Tức là \(y = \theta_n \times x_n + \theta_{n-1} \times x_{n-1} + \dots + \theta_1 \times x_1 + \theta_0 \times 1\) với \(\theta_0, \theta_1, \dots, \theta_n\) là các tham số cần tìm. Các tài liệu khác cũng hay dùng ký hiệu \(w\) (trọng số của mô hình, tiếng Anh là weight) thay vì \(\theta\).
Chúng ta sẽ từng bước xây dựng và xem xét nguyên tắc của phương pháp hồi quy tuyến tính thông qua một số ví dụ trong các mục kế tiếp.
Ước lượng \(y = ax + b\)
Không có sai số
Giả sử chúng ta có bảng dữ liệu đầu vào như sau:
| Dòng | \(x_1\) | \(y\) |
|---|---|---|
| 0 | -2 | 0 |
| 1 | 0 | -4 |
Chúng ta muốn tìm xem với \(x_1 = 2\) (không có trong bảng trên) thì sẽ nhận được giá trị \(y\) là bao nhiêu.
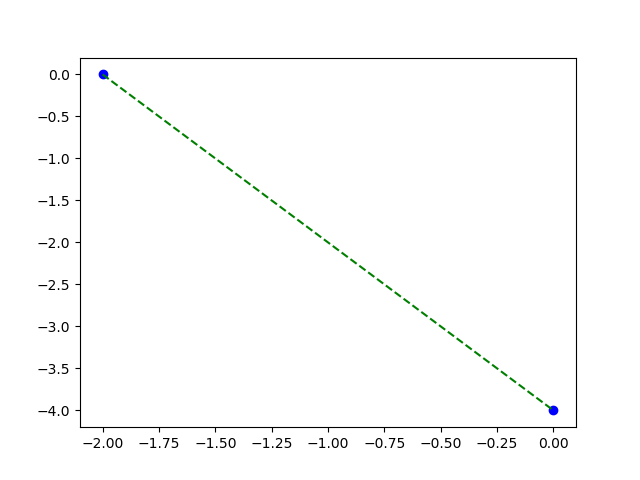
Đường thẳng đi qua chính xác hai điểm
from matplotlib import pyplot as plt
xs = [-2, 0]
ys = [0, -4]
plt.plot(xs, ys, 'bo')
plt.plot(xs, ys, 'g--')
plt.savefig('linear-reg-1.png')
Vì ta đã giả định \(y = \theta_1 x_1 + \theta_0\), và ta có đúng hai điểm đầu vào, nên cách đơn giản nhất là giải hệ phương trình để tìm ra tham số \(\theta_1, \theta_0\) của quan hệ đó. Ta sẽ có \(\theta_1 = -2, \theta_0 = -4\). Vậy nếu \(x_1 = 2\) giá trị tương ứng sẽ là \(y = -8\).
Đây chính là cách giải quyết vấn đề bình thường, khi ta phải lập trình rõ ràng từng bước cần làm để máy tính thực hiện. Nếu như bảng dữ liệu đầu vào có nhiều hơn 2 dòng thì làm sao chương trình của chúng ta tìm ra mối quan hệ giữa các điểm này?
Thêm sai số
Giả sử như bảng đầu vào của chúng ta bây giờ có thêm một số điểm mới như sau:
| Dòng | \(x_1\) | \(y\) |
|---|---|---|
| 0 | -2 | 0 |
| 1 | -1 | -3 |
| 2 | 0 | -4 |
| 3 | 1 | -3 |
Phương pháp chính xác không còn có thể được dùng nữa vì bây giờ ta có 4 điểm, và chúng không nằm trên cùng một đường thẳng nào cả.
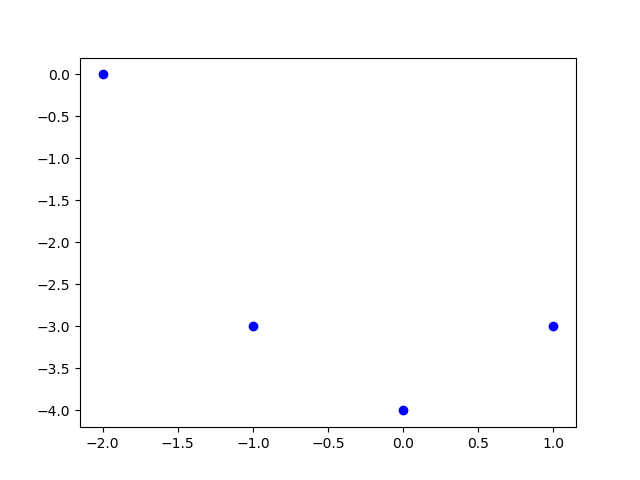
Không có đường thẳng nào đi qua 4 điểm này
from matplotlib import pyplot as plt
xs = [-2, -1, 0, 1]
ys = [0, -3, -4, -3]
plt.plot(xs, ys, 'bo')
plt.savefig('linear-reg-2.png')
Do đó, chúng ta sẽ chấp nhận có sai số trong việc hồi quy để tìm ra mối quan hệ tuyến tính giữa các điểm đầu vào.
Chúng ta giả sử rằng mối quan hệ tìm được là \(\hat{y} = \theta_1 x_1 + \theta_0 x_0\), với giá trị \(x_0 = 1\). Ký hiệu \(\hat{y}\) đọc là "y mũ" để phân biệt với "y thường", và thường được dùng để nhấn mạnh đây là giá trị phỏng đoán, không phải giá trị thực.
Sai số giữa \(\hat{y}\) và \(y\) đơn giản là \(\hat{y} - y\). Để không phải quan tâm \(\hat{y}\) lớn hơn, hay nhỏ hơn \(y\), ta sẽ dùng bình phương của sai số \((\hat{y} - y)^2\).
Với mỗi giá trị đầu vào, ta sẽ có sai số cho dòng đó. Tổng bình phương sai số (residual sum of squares, sum of squared residuals, sum of squared errors) của các dòng đầu vào thể hiện độ khớp giữa mối quan hệ tìm được, và mối quan hệ thật sự (mà chúng ta không biết). Do đó, mục tiêu của chúng ta là tìm các tham số \(\theta_1, \theta_0\) sao cho tổng bình phương sai số của các điểm là nhỏ nhất.
Gọi \(\vec{\theta} = (\theta_0, \theta_1)\) là biểu diễn dạng véc tơ của hai giá trị \(\theta_1, \theta_0\). Hàm mất mát (loss function, cost function) của phương pháp hồi quy tuyến tính có dạng:
Nhưng vì chúng ta chỉ quan tâm đến việc tìm giá trị cực tiểu của hàm mất mát, người ta thường nhân với \(\frac{1}{2}\) để khi lấy đạo hàm thì bình phương sẽ khử đi \(\frac{1}{2}\) và công thức nhìn đẹp hơn:
(Ngoài ra, nhiều tài liệu còn chia cho số dòng trong bảng đầu vào (tức là lấy trung bình cộng) để làm cho phép tính số thực trên máy tính được chính xác hơn.)
Ta cần tìm một véc tơ \(\vec{\theta_{min}}\) sao cho \(\mathcal{L}(\vec{\theta_{min}})\) có giá trị cực tiểu.
Sử dụng ký hiệu \(\mathop{\mathrm{arg\,min}}_x f(x)\) để biểu diễn một hàm trả về giá trị \(x\) mà tại đó giá trị của \(f(x)\) là nhỏ nhất, chúng ta viết lại mục tiêu của chúng ta như sau:
Một trong những cách để tìm \(\vec{\theta_{min}}\) là tính đạo hàm bậc nhất của \(\mathcal{L}(\vec{\theta})\) theo \(\vec{\theta}\) và giải phương trình để đạo hàm đó đạt giá trị 0. Tuy nhiên, cách làm này nằm ngoài phạm vi Toán phổ thông, và cần phải đến chương trình đại học đại cương về Đại số tuyến tính (Linear Algebra) và Giải tích ma trận (Matrix Calculus) chúng ta mới có thể làm.
Một cách khác để tìm \(\vec{\theta_{min}}\) là sử dụng kỹ thuật xuống dốc (gradient descent). Kỹ thuật xuống dốc có thể được sử dụng ở đây vì hàm mất mát trong trường hợp này chỉ có một cực trị toàn cục (global optimum) (và cực trị này là cực tiểu) cho nên kỹ thuật xuống dốc được đảm bảo sẽ hội tụ (converge) đến giá trị đấy. Kỹ thuật này sẽ được giải thích cặn kẽ hơn trong một bài viết khác. Ở đây, chúng ta chỉ cần tính đạo hàm riêng (partial derivative) của \(\mathcal{L}(\vec{\theta})\) theo từng biến thành phần \(\theta_1, \theta_0\) để cập nhật lại chính các biến đó.
Với \(j \in \{ 0, 1 \}\), công thức cập nhật \(\theta_j\) được cho bởi:
Hệ số \(\alpha\) được gọi là tốc độ học (learning rate). Nhiều tài liệu sử dụng \(\gamma\) hoặc \(\eta\) thay cho \(\alpha\) trong công thức trên, nhưng chúng đều có ý nghĩa như nhau cả.
Đạo hàm riêng của \(\mathcal{L}(\vec{\theta})\) theo \(\theta_j\):
Ráp vào công thức cập nhật \(\theta_j\):
Như vậy, toàn bộ việc giải ra \(\vec{\theta}\) được tóm lại ở hai bước:
- Khởi tạo các giá trị \(\theta_0, \theta_1\) ngẫu nhiên.
- Trong khi vẫn chưa hội tụ thì cập nhật \(\theta_0, \theta_1\) theo công thức trên.
Điều kiện hội tụ có thể gồm một hoặc vài điều kiện sau:
- Giá trị hàm mất mát chỉ thay đổi rất ít.
- Giá trị của \(\vec{\theta}\) thay đổi rất ít.
- Số lần lặp vượt quá một giới hạn nào đó.
- Hoặc các điều kiện khác tùy vào khả năng sáng tạo.
Ta sẽ cài đặt ý tưởng của phương pháp hồi quy tuyến tính như sau:
# Bảng đầu vào.
xs = [(1, -2), (1, -1), (1, 0), (1, 1)] # (x_0, x_1)
ys = [0, -3, -4, -3] # y
# Khởi tạo theta là vec tơ (0, 0).
theta = [0] * len(xs[0])
# Định tốc độ học.
alpha = 0.01
# Điều kiện hội tụ là lặp 1000 lần.
for _ in range(1000):
theta_new = [0] * len(theta)
for j in range(len(theta)):
# Tính độ dốc theo theta_j.
gradient = 0
for i in range(len(ys)):
y_hat = theta[1] * xs[i][1] + theta[0] * xs[i][0]
gradient += (ys[i] - y_hat) * xs[i][j]
# Cập nhật theta.
theta_new[j] = theta[j] + alpha * gradient
theta = theta_new
print(theta)
Kết quả thực thi sẽ là:
[-2.9999999999982405, -0.9999999999989124]
Tức là mối quan hệ tuyến tính giữa 4 điểm là \(\hat{y} = -3.0 \times x_1 + -1.0\). Mối quan hệ này được thể hiện qua đồ thị bên dưới.
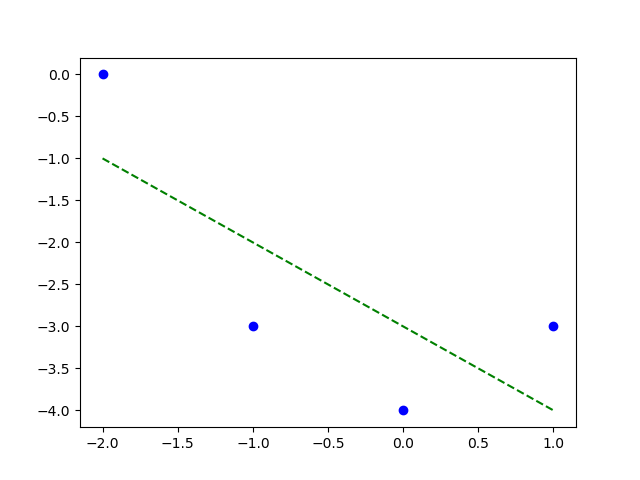
Đường khớp dữ liệu \(\theta_0 = -3.0\) và \(\theta_1 = -1.0\)
from matplotlib import pyplot as plt
xs = [-2, -1, 0, 1]
ys = [0, -3, -4, -3]
plt.plot(xs, ys, 'bo')
plt.plot([min(xs), max(xs)],
[-1.0 * min(xs) - 3.0, -1.0 * max(xs) - 3.0], 'g--')
plt.savefig('linear-reg-3.png')
Xây dựng thuộc tính (feature engineering)
Mặc dù phương pháp hồi quy tuyến tính giả định mối quan hệ tuyến tính, chúng ta vẫn có thể tìm được các mối quan hệ đa thức bậc cao, hoặc phi tuyến. Tính chất tuyến tính chỉ là giữa biến phụ thuộc và biến độc lập, còn giữa các biến độc lập với nhau thì chúng có thể có những quan hệ phi tuyến.
Xét ví dụ trong mục ở trên, với bốn điểm không thẳng hàng.
| Dòng | \(x_1\) | \(y\) |
|---|---|---|
| 0 | -2 | 0 |
| 1 | -1 | -3 |
| 2 | 0 | -4 |
| 3 | 1 | -3 |
Ta có thể thêm một cột \(x_2 = x_1^2\) để có bảng:
| Dòng | \(x_2\) | \(x_1\) | \(y\) |
|---|---|---|---|
| 0 | 4 | -2 | 0 |
| 1 | 1 | -1 | -3 |
| 2 | 0 | 0 | -4 |
| 3 | 1 | 1 | -3 |
Chúng ta muốn tìm quan hệ \(\hat{y} = \theta_2 x_2 + \theta_1 x_1 + \theta_0 x_0\) với \(x_0 = 1\). Và chúng ta chỉ cần sửa một chút mã nguồn trong phần trên:
# Bảng đầu vào.
xs = [(1, -2, 4), (1, -1, 1), (1, 0, 0), (1, 1, 1)] # (x_0, x_1, x_2)
ys = [0, -3, -4, -3] # y
# Khởi tạo theta là vec tơ (0, 0, 0).
theta = [0] * len(xs[0])
# Định tốc độ học.
alpha = 0.01
# Điều kiện hội tụ là lặp 10000 lần.
for _ in range(10000):
theta_new = [0] * len(theta)
for j in range(len(theta)):
# Tính độ dốc theo theta_j.
gradient = 0
for i in range(len(ys)):
y_hat = (theta[2] * xs[i][2] +
theta[1] * xs[i][1] +
theta[0] * xs[i][0])
gradient += (ys[i] - y_hat) * xs[i][j]
# Cập nhật theta.
theta_new[j] = theta[j] + alpha * gradient
theta = theta_new
print(theta)
Kết quả nhận được:
[-3.999999999999987, -4.7184218854317494e-15, 0.9999999999999933]
Hay viết cách khác \(\hat{y} = 1.0 \times x_2 - 0.0 \times x_1 - 4.0\). Vì \(x_2 = x_1^2\), quan hệ này là \(\hat{y} = x_1^2 - 4.0\), rõ ràng là một đường pa-ra-bôn nhị thức bậc hai.
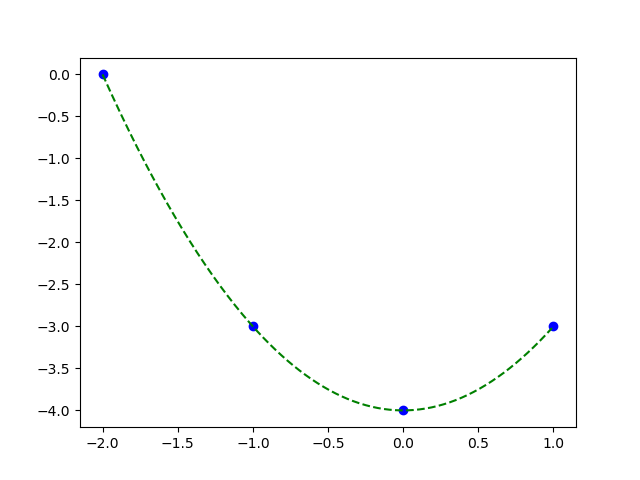
Đường pa-ra-bôn đi qua bốn điểm, cũng chính là mối quan hệ thực giữa \(y\) và \(x_1\).
from matplotlib import pyplot as plt
xs = [-2, -1, 0, 1]
ys = [0, -3, -4, -3]
plt.plot(xs, ys, 'bo')
plt.plot([x / 100.0 for x in range(min(xs) * 100, max(xs) * 100)],
[(x / 100.0)**2 - 4.0
for x in range(min(xs) * 100, max(xs) * 100)],
'g--')
plt.savefig('linear-reg-4.png')
Việc thêm cột vào bảng như chúng ta đã làm được gọi là xây dựng thuộc tính (feature engineering). Chúng ta tạo ra một thuộc tính mới, hoặc cắt bỏ đi các thuộc tính đã có nhằm giúp cho mô hình của chúng ta khớp (fit) tốt hơn với dữ liệu, hoặc đạt được một số tính chất nào đó mà chúng ta cần. Công việc xây dựng thuộc tính rất phụ thuộc vào kinh nghiệm, và sự tinh tế của người làm. Đau lòng mà nói thì nó mang tính chất mò và hên rất nhiều.
Tóm tắt
Bài viết này giới thiệu tổng quát về máy học, và xây dựng nên kỹ thuật hồi quy tuyến tính từ nền tảng. Thông qua kỹ thuật đơn giản nhưng rất phổ dụng này, chúng ta biết đến khái niệm hàm mất mát và bài toán máy học được chuyển về bài toán tối ưu hàm mất mát. Ở bài viết kế tiếp, chúng ta sẽ nói kỹ hơn về kỹ thuật xuống dốc đã được sử dụng trong việc tìm điểm cực tiểu này.
Tài liệu đọc thêm
- Tài liệu giảng trong môn CS229 Machine Learning do Dan Boneh và Andrew Ng dạy ở đại học Stanford.
- Bài 3: Linear Regression ở trang mạng Machine Learning cơ bản của Vũ Hữu Tiệp ở Đại học bang Pennsylvania (Pennsylvania State University), Hoa Kỳ.
- Scikit-learn: Linear regression ở trang mạng của Ông Xuân Hồng.
