Máy học phổ thông (8) | Python Cho Người Việt

Kỳ này chúng ta sẽ bàn về một trong những thuật toán phổ biến nhất trong loạt kỹ thuật máy học không giám sát: K-means.

Đặt vấn đề

Cho \(N\) điểm dữ liệu đầu vào, tìm cách để chia chúng ra làm \(k\) cụm/nhóm (cluster) với \(k \le N\).

Có hai điểm chính cần được nhấn mạnh:

Dữ liệu đầu vào không chứa thông tin về cụm đầu ra.
Số cụm đầu ra \(k\) là một tham số đầu vào của thuật toán.

Giá trị của tham số \(k\) phụ thuộc vào lĩnh vực cụ thể. Ví dụ trong trường học ta muốn phân học sinh ra làm 3 nhóm: học sinh giỏi, khá, và trung bình. Hoặc trong lĩnh vực quảng cáo, ta muốn phân người xem quảng cáo ra làm 2 nhóm: khách sẽ mua, và người sẽ bỏ qua.

Giải quyết vấn đề

Giả sử rằng mỗi cụm đầu ra có một tâm điểm. Cách giải quyết vấn đề đơn giản nhất là chọn ngẫu nhiên \(k\) tâm điểm và gán (assign) \(N\) điểm đầu vào vào các nhóm dựa theo khoảng cách của chúng đến \(k\) tâm điểm này.

Có nhiều cách để chọn ngẫu nhiên \(k\) tâm điểm. Ta có thể chọn ngẫu nhiên \(k\) điểm đầu vào làm tâm điểm của \(k\) nhóm. Ta cũng có thể bỏ qua bước chọn tâm điểm và nhảy thẳng đến bước gán nhóm bằng cách gán ngẫu nhiên nhóm \({1, \dots, k}\) vào \(N\) điểm đầu vào.

Dĩ nhiên cách giải này không chấp nhận được vì mỗi lần chạy sẽ cho ra kết quả rất khác với các lần chạy trước.

Thuật toán K-means khắc phục điểm yếu này bằng một bước kế: cập nhật tâm điểm dựa theo kết quả gán nhóm từ bước trước. Sau đó quá trình này được lập lại cho đến khi kết quả gán nhóm không thay đổi nữa.

Trước khi đưa ra cách cập nhật tâm điểm, chúng ta sẽ tìm hiểu thêm về mục tiêu của thuật toán K-means.

Mục đích của K-means

Giả sử ta đã gán nhóm xong. Mỗi điểm \(\vec{x^{(j)}}\) sẽ được gán vào nhóm \(i\) với tâm điểm là \(\vec{\mu^{(i)}}\). Khoảng cách Ơ-clít từ điểm \(\vec{x^{(j)}}\) đến tâm nhóm \(\vec{\mu^{(i)}}\) là \(\left \lVert \vec{x^{(j)}} - \vec{\mu^{(i)}} \right \rVert_2\) (như đã nhắc đến trong phần 7). Do đó, khoảng cách từ các điểm thuộc nhóm \(i\) bất kỳ sẽ là:

\begin{equation*} \label{eq:sum_of_cluster} \sum_{\vec{x} \in S_i}{\left \lVert \vec{x} - \vec{\mu^{(i)}} \right \rVert_2} \tag{khoảng cách nội bộ trong 1 nhóm} \end{equation*}

với \(S_i\) là tập hợp các điểm đã được gán nhóm \(i\). Do đó, với \(k\) nhóm, ta có tổng khoảng cách nội bộ của tất cả các nhóm:

\begin{equation*} \label{eq:sum_of_clusters} \sum_{i=1}^{k}\sum_{\vec{x} \in S_i}{\left \lVert \vec{x} - \vec{\mu^{(i)}} \right \rVert_2} \tag{tổng khoảng cách nội bộ của tất cả các nhóm} \end{equation*}

Mục tiêu của thuật toán K-means là tìm cách gán nhóm sao cho \(\ref{eq:sum_of_clusters}\) là nhỏ nhất. Đây là một bài toán khó, không thể giải tổng quát theo thời gian đa thức (polynomial in time).

Bước cập nhật tâm điểm của K-means

Vì bài toán tổng quát không thể giải theo thời gian đa thức nên chúng ta có thể chấp nhận lời giải gần đúng. Thay vì cực tiểu hóa \(\eqref{eq:sum_of_clusters}\), chúng ta có thể cực tiểu hóa \(\eqref{eq:sum_of_cluster}\) của từng nhóm.

Xét ví dụ với hai điểm đầu vào \(\vec{x^{(1)}}\) và \(\vec{x^{(2)}}\). Tìm điểm \(\vec{\mu}\) sao cho tổng khoảng cách từ \(\vec{x^{(1)}}\) đến \(\vec{\mu}\) và từ \(\vec{x^{(2)}}\) đến \(\vec{\mu}\) là nhỏ nhất. Một trong những giá trị phù hợp của \(\vec{\mu}\) là:

\begin{equation*} \vec{\mu} = \frac{\vec{x^{(1)}} + \vec{x^{(2)}}}{2} \end{equation*}

Điều này gợi ý rằng ở bước cập nhật của K-means, ta sẽ cập nhật tâm điểm của nhóm \(i\) thành trung bình cộng của các điểm đã được gán vào chính nhóm đó.

\begin{equation*} \vec{\mu^{(i)}} = \frac{1}{\vert S_i \vert} \sum_{\vec{x} \in S_i}\vec{x} \end{equation*}

Thuật toán K-means

Tóm lại, thuật toán K-means gồm các bước cơ bản sau:

Khởi tạo: Chọn ngẫu nhiên \(k\) điểm trong \(N\) điểm đầu vào làm tâm điểm của \(k\) nhóm.
Gán nhóm: gán nhóm \(i\) cho điểm \(j\) nếu điểm \(j\) ở gần (theo đường chim bay) tâm điểm của nhóm \(i\) nhất.
Cập nhật: tâm điểm \(i\) được cập nhật thành trung bình cộng của các điểm trong nhóm \(i\).
Lập lại bước 1 và 2 cho đến khi không còn thay đổi trong việc gán nhóm ở bước 1.

Mặc dù K-means chỉ tìm được tâm điểm tối ưu cục bộ (local optima), mà không nhất thiết là tối ưu toàn cục (global optima), nhưng kết quả nhận được từ K-means vẫn có thể phù hợp với mục đích của người dùng, hoặc dùng để làm khởi điểm cho các thuật toán khác.

Cài đặt

#!/usr/bin/env python3
import random


def distance(x, y):
    return sum((x[i] - y[i])**2 for i in range(len(x)))


def assign(xs, centroids):
    assignments = [0] * len(xs)
    for j in range(len(xs)):
        x = xs[j]
        m = distance(x, centroids[0])
        for i in range(1, len(centroids)):
            d = distance(x, centroids[i])
            if d < m:
                m = d
                assignments[j] = i
    return assignments


def update(xs, centroids, assignments):
    nr_elements_in_cluster = [0] * len(centroids)
    sums = [[0.0] * len(xs[0]) for _ in centroids]
    for j, x in enumerate(xs):
        i = assignments[j]
        nr_elements_in_cluster[i] += 1
        for d in range(len(x)):
            sums[i][d] += x[d]
    for i, s in enumerate(sums):
        for d in range(len(s)):
            s[d] /= nr_elements_in_cluster[i]
    return sums


def k_means(xs, k):
    history = []
    # Lấy ngẫu nhiên k điểm làm tâm điểm.
    centroids = [xs[i][:] for i in random.sample(range(len(xs)), k)]
    history.append(centroids)
    old_assignments = None
    assignments = None
    while (assignments is None) or old_assignments != assignments:
        # Bước 1: Gán nhóm.
        old_assignments = assignments
        assignments = assign(xs, centroids)
        if old_assignments == assignments:
            break
        # Bước 2: Cập nhật tâm điểm.
        centroids = update(xs, centroids, assignments)
        history.append(centroids)
    return history


xs = (
    (-1, 0), (1, 0), (0, 1), (0, -1), (0, 0),
    (9, 0), (11, 0), (10, 1), (10, -1), (10, 0),
)
history = k_means(xs, 2)
for c in history:
    print(c)

Khi chạy đoạn mã này, kết quả nhận được có thể là:

[(10, 1), (9, 0)]
[[10.333333333333334, 0.3333333333333333], [2.7142857142857144, -0.14285714285714285]]
[[10.0, 0.0], [0.0, 0.0]]

Ta thấy rằng hai tâm điểm được chọn ngẫu nhiên, sau đó được cập nhật, và cuối cùng hội tụ tại hai tâm điểm đúng ý muốn.

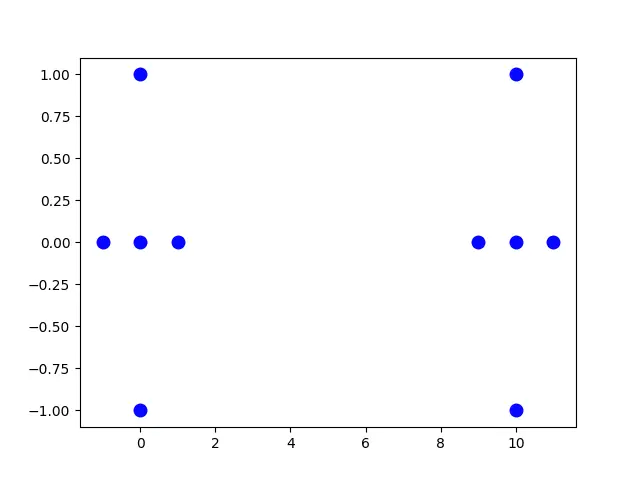
Sự hội tụ của các tâm điểm

# Tiếp tục mã nguồn phía trên.
from matplotlib import pyplot as plt
from matplotlib import animation


def run(t):
    global c1, c2, history
    if t <= 1:
        return
    if t % 2 == 0:
        if c1 is None:
            c1 = ax.plot([history[0][0][0]], [history[0][0][1]], 'x', mew=4, color='r')[0]
            c2 = ax.plot([history[0][1][0]], [history[0][1][1]], '+', mew=4, color='y')[0]
        else:
            i = t // 2 - 1
            c1.set_data([history[i][0][0]], [history[i][0][1]])
            c2.set_data([history[i][1][0]], [history[i][1][1]])

fig, ax = plt.subplots()
ax.plot([x[0] for x in xs], [x[1] for x in xs], 'o', mew=4, color='b')
c1 = None
c2 = None

anim = animation.FuncAnimation(fig, run, repeat=False, frames=2 + 2*len(history))
anim.save('k-means.gif', writer='imagemagick')

Tóm tắt

Thuật toán K-means là một thuật toán máy học không giám sát dùng để phân nhóm các điểm đầu vào. Thuật toán này gồm 2 bước chính là gán nhóm, và cập nhật tâm điểm. Hai bước này được lập lại cho đến khi việc gán nhóm không còn thay đổi nữa. Tác giả hy vọng bạn đọc nhận ra được sự đơn giản của thuật toán, thậm chí có thể cảm nhận được rằng cá nhân mình cũng có thể sáng tạo được các bước đã bàn qua. Sự đơn giản từ trực giác này chính là nguyên nhân K-means trở thành một trong những thuật toán được sử dụng rộng rãi nhất trong lĩnh vực máy học, mặc dù K-means không đảm bảo kết quả tốt trong mọi trường hợp.

Tài liệu đọc thêm

Trang mạng Wikipedia về "k-means clustering" tại https://en.wikipedia.org/wiki/K-means_clustering.