Giới thiệu về kỹ thuật xuống dốc (gradient descent)

Trong phần 1, chúng ta sử dụng kỹ thuật xuống dốc để tìm điểm cực tiểu của hàm mất mát trong phương pháp hồi quy tuyến tính. Phần 2 của loạt bài Máy học phổ thông sẽ xem xét kỹ thuật xuống dốc cặn kẽ hơn.

Kỹ thuật xuống dốc là một thuật toán tối ưu hóa (optimization algorithm) để tìm giá trị cực tiểu của một hàm. Như nhiều thuật toán tối ưu hóa khác, kỹ thuật xuống dốc lặp đi lặp lại một thủ tục tính toán để tìm ra giá trị kế tiếp, thường là tốt hơn, từ giá trị hiện tại.

Vì không phải là thuật toán chính xác, kỹ thuật xuống dốc không hứa hẹn trả về giá trị cực tiểu toàn cục (global minimum) mà chỉ có khả năng cao sẽ tìm thấy giá trị cực tiểu cục bộ (local minimum). Mặc dù có khuyết điểm lớn này nhưng trong thực tế kỹ thuật xuống dốc vẫn được sử dụng nhiều bởi vì:

  1. Hàm cần tìm giá trị cực tiểu thường đơn giản và chỉ có một vài, hoặc thậm chí chỉ có duy nhất, cực tiểu. Như đã xét qua ở phần 1, hàm mất mát của hồi quy tuyến tính chỉ có duy nhất một cực tiểu.
  2. Chúng ta có thể thực hiện kỹ thuật xuống dốc nhiều lần với nhiều vị trí khởi đầu ngẫu nhiên, và chọn lại giá trị cực tiểu đã tìm được trong tất cả các lần xuống dốc.
  3. Trong nhiều bài toán, lời giải chính xác không quan trọng bằng lời giải tốt vừa đủ. Chúng ta sẽ thấy rằng trong máy học, sự gần đúng được tận dụng rất nhiều. Suy cho cùng, ai có thể đoán được giá nhà trong tương lai một cách chính xác? Chúng ta chỉ có thể ước lượng gần đúng mà thôi.

Với những điều trên, chúng ta sẽ xem xét kỹ thuật xuống dốc thông qua một vài ví dụ cụ thể.

Tìm điểm cực tiểu của một pa-ra-bôn

Lập ra công thức xuống dốc

Một trong những bài toán thường gặp ở chương trình phổ thông là khảo sát hàm số. Bạn đọc chắc chắn đã quá quen thuộc với việc vẽ đồ thị pa-ra-bôn, hoặc tạo bảng biến thiên. Chúng ta sẽ bắt đầu từ đó.

Gọi hàm \(y = x^2 - 2x - 5\). Đạo hàm bậc nhất của hàm này là \(y^\prime = 2x - 2\), có nghiệm tại \(x = 1\). Đồ thị của hàm này được thể hiện trong hình sau.

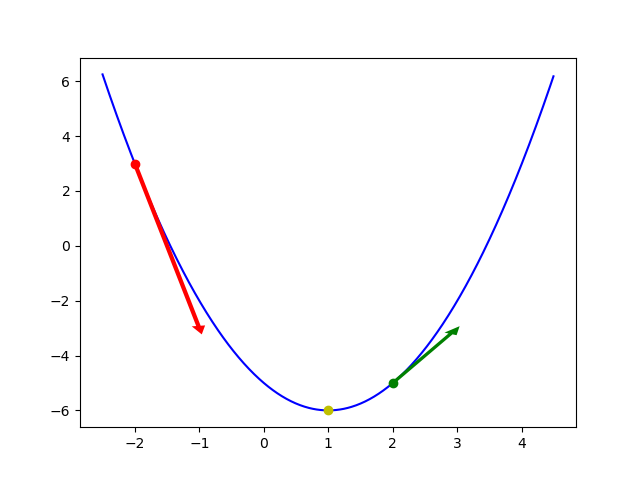
Đồ thị và tiếp tuyến tại ba điểm

import math
from matplotlib import pyplot as plt

def f(x):
    return x**2 - 2*x - 5

def f_prime(x):
    return 2*x - 2

def tangent(x0):
    slope = f_prime(x0)
    angle = math.atan(slope)
    magnitude = int(abs(slope))
    y0 = f(x0)
    dx = magnitude * math.cos(angle)
    dy = dx * slope
    return x0, y0, dx, dy

xs = list(x / 100.0 for x in range(-250, 450))
ys = [f(x) for x in xs]
plt.plot(xs, ys, 'b-')
plt.plot([1], [f(1)], 'yo')
plt.arrow(*tangent(-2), width=0.07, fc='red', ec='none', zorder=2)
plt.plot(*tangent(-2)[:2], marker='o', color='red', zorder=3)
plt.arrow(*tangent(2), width=0.07, fc='green', ec='none', zorder=2)
plt.plot(*tangent(2)[:2], marker='o', color='green', zorder=3)
plt.savefig('gradient-descent-1.png')

Nếu chúng ta lập bảng biến thiên, chúng ta sẽ có bảng sau:

\begin{equation*} \begin{array}{c|cccccc} x & -\infty & & & & +\infty \\ \hline f^\prime(x) & & - & 1 & + & & \\ \hline f(x) & +\infty & & & & +\infty \\ & & \searrow & & \nearrow & \\ & & & -6 & & \end{array} \end{equation*}

Dựa vào bảng biến thiên, ta thấy rằng giá trị của hàm giảm xuống khi biến số tiến từ \(-\infty\) đến nghiệm của đạo hàm bậc nhất và tăng lên khi biến số tiếp tục tiến về \(+\infty\). Dựa vào đồ thị, ta thấy độ tăng hay giảm giá trị của hàm (trên trục \(y\)) phụ thuộc vào góc của tiếp tuyến, cũng là giá trị của đạo hàm bậc nhất. Tổng hợp hai nhận xét này, chúng ta đi đến kết luận chủ đạo của kỹ thuật xuống dốc:

  1. Khi giá trị của đạo hàm bậc nhất là âm (tức là dốc xuống), ta cần tăng giá trị của biến (đi xuống theo dốc). Khi giá trị đó là dương (tức là dốc lên), ta cần giảm giá trị của biến (đi xuống ngược dốc). Nói một cách khác, giá trị biến cần phải thay đổi theo chiều ngược lại so với dấu của đạo hàm. Đây là lý do của tên gọi của kỹ thuật này.
  2. Ta có thể dùng giá trị của đạo hàm bậc nhất để điều chỉnh độ tăng / giảm của biến.

Từ hai kết luận chủ đạo đó, ta lập ra công thức cập nhật biến theo kỹ thuật xuống dốc như sau:

\begin{equation*} x^{(t+1)} = x^{(t)} - \alpha \times f^\prime \left( x^{(t)} \right) \end{equation*}

Ký hiệu \(x^{(t)}\) có nghĩa là giá trị của biến \(x\) tại thời điểm \(t\). Dấu trừ trong công thức trên thể hiện điểm 1, và tích của \(\alpha\) với đạo hàm bậc nhất thể hiện điểm 2.

Hệ số \(\alpha > 0\) được gọi là tốc độ học (learning rate). Nhiều tài liệu khác sử dụng ký hiệu \(\eta\) hay \(\gamma\) để chỉ cùng một ý. Khi tốc độ học lớn, sự thay đổi của biến cũng cao, và ngược lại. Trong thực tế, tốc độ học thường được làm giảm dần (decay) theo thời gian nhằm tránh trường hợp biến nhảy qua nhảy lại ở hai bên điểm cực tiểu.

Cuối cùng, cài đặt kỹ thuật xuống dốc để tìm điểm cực tiểu trong ví dụ này đơn giản như sau:

import random
import sys

def f_prime(x):
    return 2*x - 2

# Chọn ngẫu nhiên giá trị ban đầu của x.
x = random.randint(-sys.maxint, sys.maxint)
# Chọn alpha vừa phải.
alpha = 0.1
# Lặp 1000 lần.
for _ in range(1000):
    x = x - alpha * f_prime(x)
print(x)

Kết quả nhận được khi chạy chương trình này trùng khớp với điểm cực tiểu:

1.0

Xem xét ảnh hưởng của tốc độ học

Đoạn ảnh sau minh họa ảnh hưởng của hệ số \(\alpha\) đến việc xuống dốc. Hai điểm đỏ và xanh lá cây ở trong hình đều xuất phát cùng một chỗ. Ở bên trái, với tốc độ học thấp, chúng ta thấy điểm đỏ di chuyển khá chậm. Ở bên phải, với tốc độ học cao hơn, ta thấy điểm xanh chỉ chuyển từ nhánh phải qua nhánh trái mà không thật sự đi xuống.

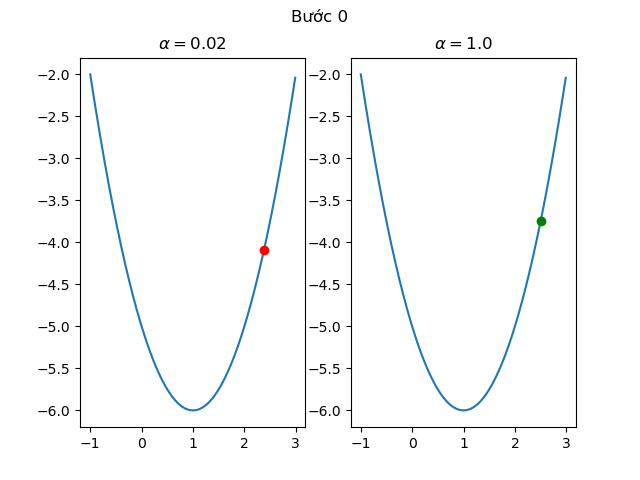
Ảnh hưởng của tốc độ học

# encoding: utf-8
from matplotlib import pyplot as plt
from matplotlib import animation

def f(x):
    return x**2 - 2*x - 5

def f_prime(x):
    return 2*x - 2

def run(t):
    global dot1, dot2, x_slow, x_bounce
    x_slow = x_slow - 0.02 * f_prime(x_slow)
    x_bounce = x_bounce - 1.0 * f_prime(x_bounce)
    dot1.set_data([x_slow], [f(x_slow)])
    dot2.set_data([x_bounce], [f(x_bounce)])
    plt.suptitle(u'Bước {}'.format(t))

# Cùng bắt đầu từ một điểm.
x_slow = 2.5
x_bounce = 2.5
xs = list(range(-100, 300))

fig, (ax1, ax2) = plt.subplots(1, 2)

ax1.plot([x / 100.0 for x in xs], [f(x / 100.0) for x in xs])
ax1.set_title(r'$\alpha = 0.02$')
dot1 = ax1.plot([x_slow], [f(x_slow)], 'ro')[0]

ax2.plot([x / 100.0 for x in xs], [f(x / 100.0) for x in xs])
ax2.set_title(r'$\alpha = 1.0$')
dot2 = ax2.plot([x_bounce], [f(x_bounce)], 'go')[0]

anim = animation.FuncAnimation(fig, run, repeat=False, frames=40)
anim.save('gradient-descent-2.gif', writer='imagemagick')

Tìm điểm cực tiểu của hàm bậc 4

Ví dụ kế tiếp của chúng ta là một hàm bậc 4. Chúng ta sẽ xem xét hàm \(y = x^4 + 4x^3 + x^2 - 4x + 3\). Đạo hàm bậc nhất là \(y^\prime = 4x^3 + 12x^2 + 2x - 4\). Đồ thị của hàm này được thể hiện trong hình bên dưới.

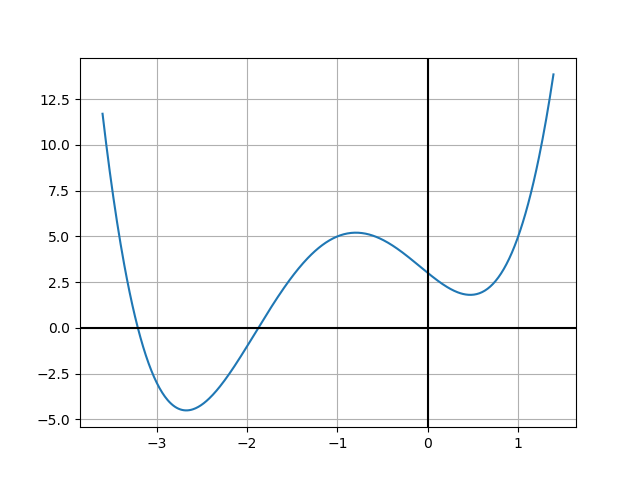
Đồ thị hàm bậc 4 với hai cực tiểu

from matplotlib import pyplot as plt

def f(x):
    return x**4 + 4*x**3 + x**2 - 4*x + 3

xs = [x / 100.0 for x in range(-360, 140)]
ys = [f(x) for x in xs]
plt.plot(xs, ys)
plt.grid()
plt.axhline(y=0, color='black')
plt.axvline(x=0, color='black')
plt.savefig('gradient-descent-3.png')

Cực tiểu cục bộ và cực tiểu toàn cục

Chúng ta thấy rằng đồ thị trên có hai điểm cực tiểu cục bộ. Điểm cực tiểu cục bộ bên trái cũng là điểm cực tiểu toàn cục. Hình sau minh họa kỹ thuật xuống dốc với bốn điểm khởi đầu ngẫu nhiên.

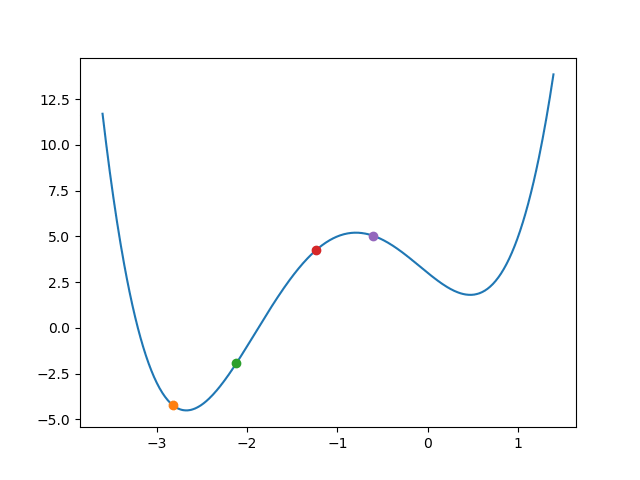
Xuống dốc với khởi đầu ngẫu nhiên

import random
import sys
from matplotlib import pyplot as plt
from matplotlib import animation

def f(x):
    return x**4 + 4*x**3 + x**2 - 4*x + 3

def f_prime(x):
    return 4*x**3 + 12*x**2 + 2*x - 4

def run(t):
    global alpha, dot_xs, dots
    [dot.set_data([x], [f(x)]) for dot, x in zip(dots, dot_xs)]
    for i in range(len(dot_xs)):
        dot_xs[i] = dot_xs[i] - alpha * f_prime(dot_xs[i])

# Khởi tạo ngẫu nhiên.
xs = list(range(-360, 140))
nr_dots = 4
dot_xs = [random.randint(min(xs), max(xs) - 1) / 100.0 for _ in range(nr_dots)]
alpha = 0.01

fig, ax = plt.subplots()
ax.plot([x / 100.0 for x in xs], [f(x / 100.0) for x in xs])
dots = [ax.plot([x], [f(x)], 'o')[0] for x in dot_xs]

anim = animation.FuncAnimation(fig, run, repeat=False, frames=40)
anim.save('gradient-descent-4.gif', writer='imagemagick')

Ta thấy rằng tùy vào vị trí khởi đầu mà điểm tròn có thể lọt vào cực tiểu cục bộ hay cực tiểu toàn cục. Nhận xét này dẫn đến một cách đơn giản để tăng cao tỷ lệ tìm được cực tiểu toàn cục: lập lại việc xuống dốc nhiều lần với khởi điểm khác nhau.

Ảnh hưởng khác của tốc độ học

Ví dụ đầu tiên trong bài viết này đã cho thấy ảnh hưởng của tốc độ học đến việc hội tụ của kỹ thuật xuống dốc. Trong ví dụ này, chúng ta sẽ thấy một ảnh hưởng khác của tốc độ học.

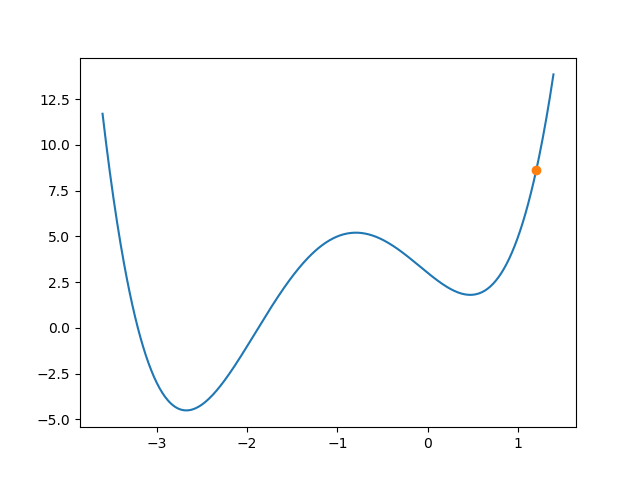
Tốc độ học lớn có thể giúp nhảy qua hố

from matplotlib import pyplot as plt
from matplotlib import animation

def f(x):
    return x**4 + 4*x**3 + x**2 - 4*x + 3

def f_prime(x):
    return 4*x**3 + 12*x**2 + 2*x - 4

def run(t):
    # Chờ 10 khung hình đầu tiên.
    if t < 10:
        return
    global alpha, dot_x, dot
    dot.set_data([dot_x], [f(dot_x)])
    dot_x = dot_x - alpha * f_prime(dot_x)

dot_x = 1.2
alpha = 0.12
xs = list(range(-360, 140))

fig, ax = plt.subplots()
ax.plot([x / 100.0 for x in xs], [f(x / 100.0) for x in xs])
dot = ax.plot([dot_x], [f(dot_x)], 'o')[0]

anim = animation.FuncAnimation(fig, run, repeat=False, frames=40)
anim.save('gradient-descent-5.gif', writer='imagemagick')

Chúng ta thấy là sự thay đổi lớn (vì tốc độ học lớn) có thể giúp thoát ra khỏi hố cực tiểu cục bộ. Tuy nhiên, tốc độ học lớn cũng dẫn đến việc hội tụ khó khăn hơn. Để giải quyết vấn đề hội tụ, người ta thường giảm (decay) tốc độ học theo thời gian. Việc này sẽ làm cho sự thay đổi của biến qua các bước giảm dần, dẫn đến việc hạn chế hiện tượng nhảy qua nhảy lại như trong hình.

Có nhiều phương thức giảm tốc độ học theo thời gian. Không có phương thức nào tốt hơn phương thức nào. Chúng ta cần thử với tất cả để chọn ra cách tốt nhất cho mục đích của mình. Một vài phương thức phổ dụng:

Sử dụng hằng số
Đôi khi chúng ta không cần phải thay đổi tốc độ học theo thời gian. Sử dụng một hằng số đã đủ để giải quyết vấn đề.
Giảm theo thời gian
Ta có thể giảm tốc độ học theo công thức, ví dụ như \(\alpha = \alpha_0 \times \cfrac{1}{1 + t}\). Ở đây \(t\) là số bước đã chạy.
Giảm theo hàm bậc thang (step function)
Tương tự như giảm theo thời gian nhưng ta sẽ giữ tốc độ học hiện tại lâu hơn một tí. Ví dụ như ta có thể giảm tốc độ học từ 1.0 xuống 0.1 sau 10 bước chạy, rồi xuống 0.01 sau 100 bước kế.

Tóm lại, cũng như nhiều tham số khác, việc xác định tốc độ học thích hợp vẫn chủ yếu dựa vào kết quả của nhiều thử nghiệm.

Tìm điểm cực tiểu của hàm đa biến

Trong hai ví dụ trên, chúng ta xét hàm đơn biến theo dạng \(y = f(x)\). Trong ví dụ này chúng ta sẽ xét ví dụ hàm đa biến \(z = f(x, y) = x^2 + y^2\).

Vì đây là hàm đa biến, sự thay đổi của từng biến sẽ ảnh hưởng đến sự thay đổi chung của hàm. Do đó, chúng ta không thể xuống dốc theo từng biến riêng biệt (tức là xuống dốc theo \(x\) trước, rồi sau đó theo \(y\)) mà phải xuống dốc theo tất cả các biến cùng một lúc.

Định nghĩa dốc (gradient)

Dốc còn được biết đến như là sự biến thiên tại chỗ ở một điểm, khác với sự biến thiên tổng quát theo khoảng giá trị như trong bảng biến thiên. Nhiều tài liệu để nguyên từ tiếng Anh và dịch là gra-di-en.

Ở hai ví dụ trên, độ dốc của hàm đơn biến là đạo hàm bậc nhất của biến, hướng được quy định bởi dấu của đạo hàm (âm hướng xuống, dương hướng lên). Với hàm đa biến, dốc được xác định bởi sự thay đổi của từng biến. Với cách ghi dạng véc tơ, dốc của hàm \(f\) được viết là \(\vec{\nabla} f\) hoặc \(\nabla f\) là một véc tơ với mỗi phần tử là dốc của biến tương ứng.

\begin{equation*} \nabla f(x_1, \dots, x_n) = \left( \cfrac{\partial f}{\partial x_1}, \dots, \cfrac{\partial f}{\partial x_n} \right) \end{equation*}

Do đó, kỹ thuật xuống dốc của hàm đa biến được viết theo dạng véc tơ:

\begin{equation*} \left( x_1^{(t+1)}, \dots, x_n^{(t+1)} \right) = \left( x_1^{(t)}, \dots, x_n^{(t)} \right) - \alpha \times \nabla f \left( x_1^{(t)}, \dots, x_n^{(t)} \right) \end{equation*}

Hay theo từng biến với \(j \in \{ 1, \dots, n \}\):

\begin{equation*} x_j^{(t+1)} = x_j^{(t)} - \alpha \times \cfrac{\partial}{\partial x_j} f \left( x_1^{(t)}, \dots, x_n^{(t)} \right) \end{equation*}

Cài đặt kỹ thuật xuống dốc để tìm cực tiểu của hàm \(z = x^2 + y^2\) như sau:

import random
import sys

def f_prime_x(x, y):
    return 2*x

def f_prime_y(x, y):
    return 2*y

x = random.randint(-sys.maxint, sys.maxint)
y = random.randint(-sys.maxint, sys.maxint)
alpha = 0.1
for _ in range(1000):
    x, y = x - alpha * f_prime_x(x, y), y - alpha * f_prime_y(x, y)
print(x, y)

Khi chạy đoạn mã này ta sẽ thấy kết quả tương tự như sau:

(1.9555628848697857e-88, -1.3023401849027657e-88)

Điểm cực trị đúng là tại \((0, 0)\).

Hình bên dưới minh họa việc xuống dốc từ điểm \((2.5, 2.5)\). Điểm vàng chỉ xuống dốc theo biến \(x\), điểm xanh lá cây chỉ xuống dốc theo biến \(y\) và điểm xanh da trời xuống dốc theo cả hai biến.

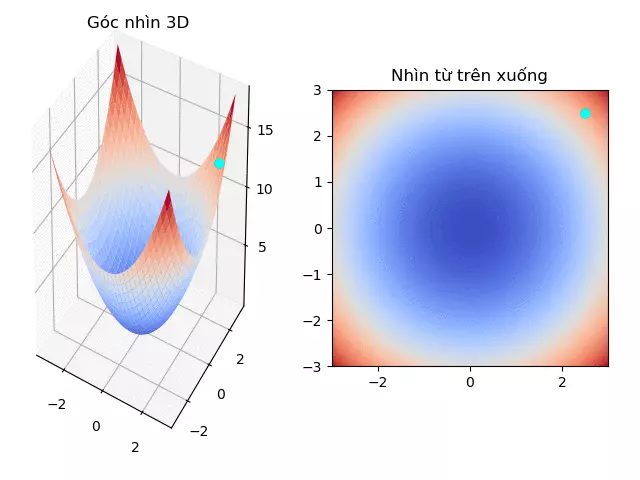
Xuống dốc hàm đa biến \(z = x^2 + y^2\)

# encoding: utf-8
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import animation
from matplotlib import cm
from matplotlib import pyplot as plt
import numpy as np

def f(x, y):
    return x**2 + y**2

def f_prime(v):
    return 2*v

alpha = 0.05
X = np.arange(-3, 3.1, 0.1)
Y = np.arange(-3, 3.1, 0.1)
X, Y = np.meshgrid(X, Y)
Z = f(X, Y)

fig = plt.figure()
fig.subplots_adjust(left=0, bottom=0.05, right=0.95, top=1.0,
                    wspace=None, hspace=None)
ax = fig.add_subplot(121, projection='3d')
bx = fig.add_subplot(122, aspect='equal')
ax.plot_surface(X, Y, Z, cmap=cm.coolwarm)
ax.set_title(u'Góc nhìn 3D')
bx.contourf(X, Y, Z, 100, cmap=cm.coolwarm)
bx.set_title(u'Nhìn từ trên xuống')

x0 = y0 = 2.5
x = x0
y = y0
z = f(x, y)

dot_a_x = ax.plot3D([x], [y], [z], 'o', color='yellow')[0]
dot_a_y = ax.plot3D([x], [y], [z], 'o', color='green')[0]
dot_a = ax.plot3D([x], [y], [z], 'o', color='cyan')[0]

dot_b_x = bx.plot([x], [y], 'o', color='yellow')[0]
dot_b_y = bx.plot([x], [y], 'o', color='green')[0]
dot_b = bx.plot([x], [y], 'o', color='cyan')[0]

def run(t):
    if t <= 5:
        return
    global x, y
    x = x - alpha * f_prime(x)
    y = y - alpha * f_prime(x)
    dot_a.set_data([x], [y])
    dot_a.set_3d_properties([f(x, y)])
    dot_a_x.set_data([x], [y0])
    dot_a_x.set_3d_properties([f(x, y0)])
    dot_a_y.set_data([x0], [y])
    dot_a_y.set_3d_properties([f(x0, y)])
    dot_b.set_data([x], [y])
    dot_b_x.set_data([x], [y0])
    dot_b_y.set_data([x0], [y])

anim = animation.FuncAnimation(fig, run, repeat=False, frames=50)
anim.save('gradient-descent-6.gif', writer='imagemagick')

Tóm tắt

Trong bài viết này, chúng ta đã thiết lập nên kỹ thuật xuống dốc dựa vào những nhận xét trực giác về mối quan hệ giữa dốc của hàm và giá trị cực tiểu. Nếu dốc đi lên, chúng ta cần giảm giá trị biến, và nếu dốc đi xuống, chúng ta cần tăng giá trị biến. Chúng ta cũng xem qua ảnh hưởng của hệ số \(\alpha\) (hay tốc độ học) đến sự xuống dốc, và nhắc đến một số điều chỉnh nhằm làm cho việc xuống dốc có hiệu quả cao hơn. Cuối cùng, chúng ta đã tổng quát hóa kỹ thuật xuống dốc cho hàm đơn biến để áp dụng cho hàm đa biến.

Một điều quan trọng chúng ta có thể nhận ra là kỹ thuật xuống dốc không đảm bảo sẽ đưa lại kết quả đúng. Các cách giảm tốc độ học cũng không thể đảm bảo điều gì. Đau lòng mà nói thì các kỹ thuật đã trình bày trong bài này chỉ mang tính gần đúng, nhưng trong rất nhiều trường hợp thì giá trị gần đúng cũng có thể đáp ứng được nhu cầu đặt ra.

Kỹ thuật xuống dốc được trình bày ở đây là cách đơn giản nhất. Có nhiều biến thể của kỹ thuật này nhằm làm giảm lượng tính toán, tăng tốc độ hội tụ. Bạn đọc có thể tham khảo thêm trong các tài liệu được liệt kê ở cuối bài.

Cuối cùng, để tìm cực đại của một hàm, ta có thể dùng kỹ thuật lên dốc (gradient ascent). Sự thay đổi duy nhất là chuyển dấu trừ trong công thức xuống dốc thành dấu cộng, tức là nếu dốc đi lên, thì ta đi lên theo dốc, nếu dốc đi xuống, thì ta đi lên ngược dốc.

Tài liệu đọc thêm

  1. Tài liệu giảng trong môn CS168: Modern Algorithmic Toolbox do Tim Roughgarden và Greg Valiant dạy ở đại học Stanford.
  2. Bài giảng Gradient Descent trong môn Machine Learning do Andrew Ng dạy ở Coursera.
  3. Bài 7: Gradient Descent (phần 1/2) và Bài 8: Gradient Descent (phần 2/2) ở trang mạng Machine Learning cơ bản của Vũ Hữu Tiệp ở Đại học bang Pennsylvania (Pennsylvania State University), Hoa Kỳ.